Experiment Design Heuristics

Using Heuristics in Updater Loops

During an experiment, the current posterior distribution represented by an SMCUpdater instance can be used to adaptively make decisions about which measurements should be performed. For example, utility functions such as the information gain and negative variance can be used to choose optimal measurements.

On the other hand, this optimization is generally quite computationally expensive, such that many less optimal measurements could have been performed before an optimization step completes. Philosophically, there are no “bad” experiments, in that even suboptimal measurements can still carry useful information about the parameters of interest.

In light of this, it can be substantially less expensive to use a heuristic function of prior information to select experiments without explicit optimization. For example, consider the single-parameter inversion precession model with model parameters \(\vec{x} = (\omega)\), experiment parameters \(e = (\omega_-, t)\) and likelihood function

\[\Pr(1 | \omega; \omega_-, t) = \sin^2([\omega - \omega_-] t / 2).\]

For a given posterior distribution, the particle guess heuristic (PGH) [WGFC13a] then chooses \(\omega_-\) and \(t\) for the next experiment by first sampling two particles \(\omega_-\) and \(\omega_-'\) from the posterior. The PGH then assigns the time \(t = 1 / |\omega_- \omega_-'|\).

QInfer implements heuristics as subtypes of Heuristic, each of which take an updater and can be called to produce experimental parameters. For example, the PGH is implemented by the class PGH, and can be used in an updater loop to adaptively select experiments.

model = SimpleInversionModel()
prior = UniformDistribution([0, 1])
updater = SMCUpdater(model, 1000, prior)
heuristic = PGH(updater, inv_field='w_', t_field='t')

true_omega = prior.sample()

ts = []
est_omegas = []

for idx_exp in range(100):
    experiment = heuristic()
    datum = model.simulate_experiment(true_omega, experiment)
    updater.update(datum, experiment)

    ts.append(experiment['t'])
    est_omegas.append(updater.est_mean())

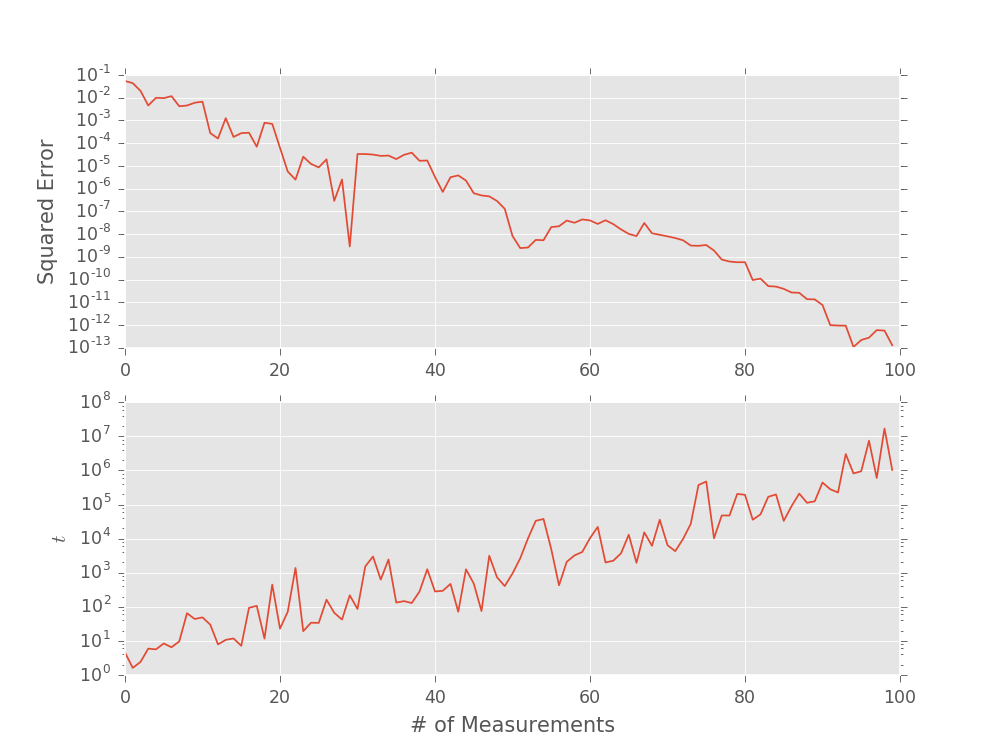
ax = plt.subplot(2, 1, 1)
plt.semilogy((est_omegas - true_omega) ** 2)
plt.ylabel('Squared Error')

plt.subplot(2, 1, 2, sharex=ax)
plt.semilogy(ts)
plt.xlabel('# of Measurements')
plt.ylabel('$t$')

plt.show()

(Source code, svg, pdf, hires.png, png)

../_images/heuristics-1.png

Changing Heuristic Parameters

Essentially, heuristics in QInfer are functions that take SMCUpdater instances and return functions that then yield experiments. This design allows for specializing heuristics by providing other arguments along with the updater. For instance, the ExpSparseHeuristic class implements exponentially-sparse sampling \(t_k = ab^k\) for SimplePrecessionModel. Both \(a\) and \(b\) are parameters of the heuristic, named scale and base, respectively. Thus, it is easy to override the defaults to obtain different heuristics.

model = SimplePrecessionModel()
prior = UniformDistribution([0, 1])
updater = SMCUpdater(model, 1000, prior)
heuristic = ExpSparseHeuristic(updater, scale=0.5)

true_omega = prior.sample()
est_omegas = []

for idx_exp in range(100):
    experiment = heuristic()
    datum = model.simulate_experiment(true_omega, experiment)
    updater.update(datum, experiment)

    est_omegas.append(updater.est_mean())

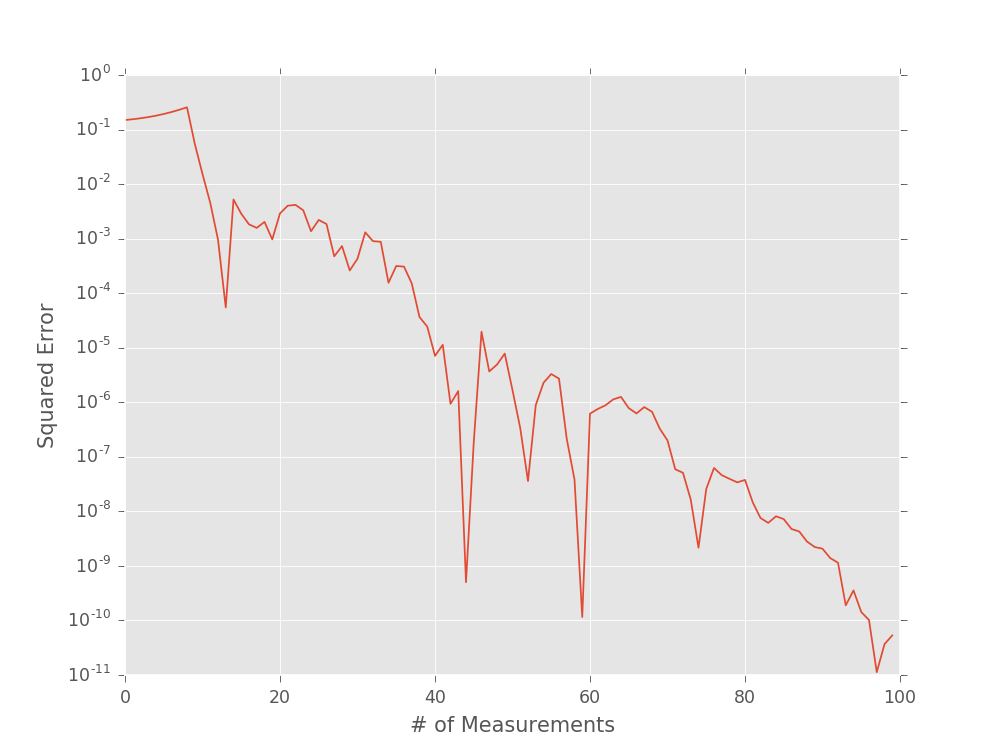
plt.semilogy((est_omegas - true_omega) ** 2)
plt.xlabel('# of Measurements')
plt.ylabel('Squared Error')

plt.show()

(Source code, svg, pdf, hires.png, png)

../_images/heuristics-2.png

In overriding the default parameters of heuristics, the functools.partial() function provided with the Python standard library is especially useful, as it allows for easily making new heuristics with different default parameter values:

>>> from qinfer import ExpSparseHeuristic
>>> from functools import partial
>>> rescaled_heuristic_class = partial(ExpSparseHeuristic, scale=0.01)

Later, once we have an updater, we can then make new instances of our rescaled heuristic.

>>> heuristic = rescaled_heuristic_class(updater)

This technique is especially useful in Performance Testing, as it makes it easy to modify existing heuristics by changing default parameters through partial application.